I read papers “Attention Is All You Need”, “Neural Machine Translation by Jointly Learning to Align and Translate” and checked codes for nano-GPT. Following is my understandings of the transformer architecture.

Transformer architecture

The transformer architecture generally has a encoder-decoder structure. Suppose the original text input is [x1, ..., xn]. Encoder tries to encode the orginal text input into an inner representation [z1, ..., zn] and decoder reconstructs the ouptut [y1, ..., yn] based on the inner representations. Here is an overview graph of such architecture:

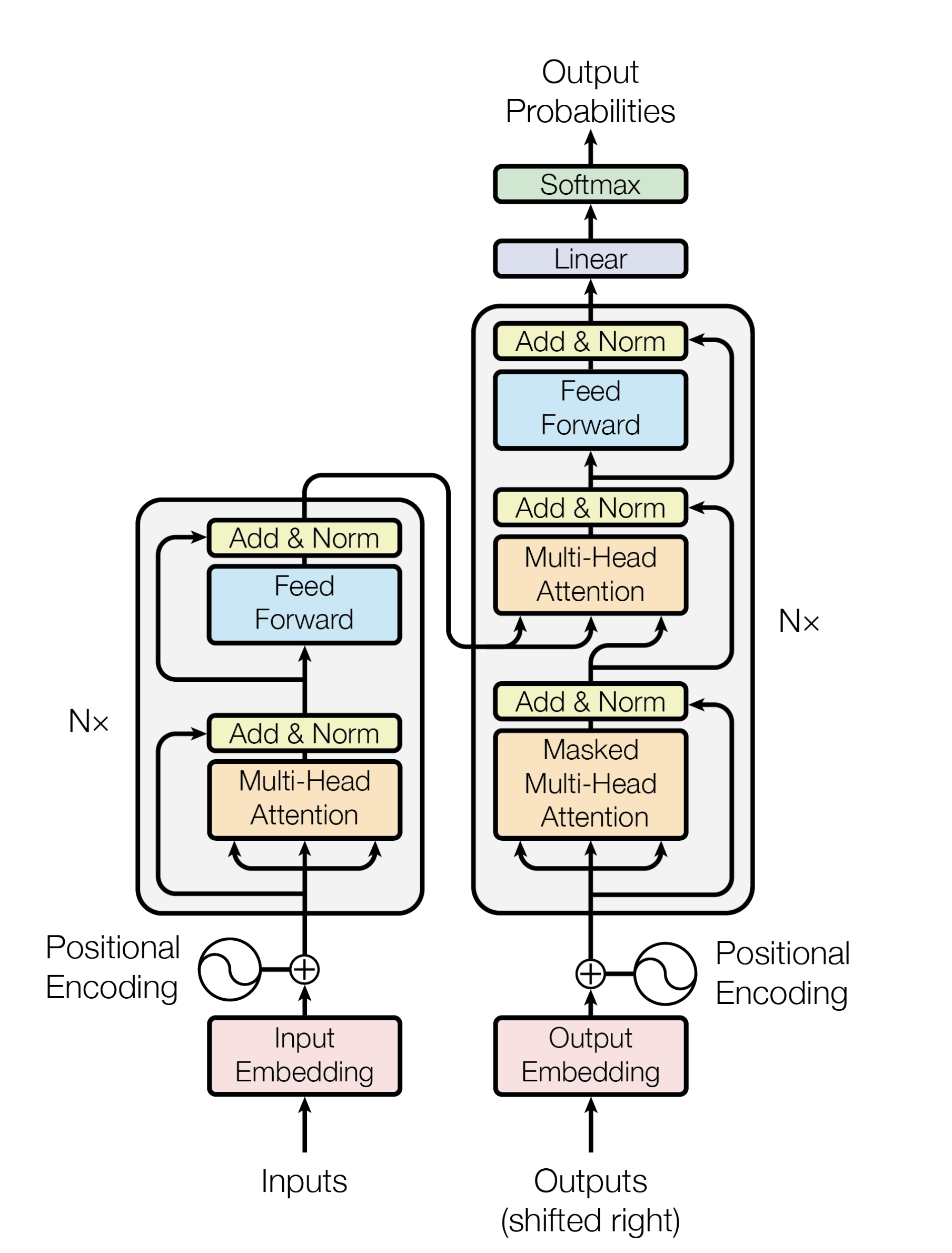
Transformer Encoder

An encoder consists of h identical building blocks which connects with each other in sequential. The basic building block consists of two sub-layers where the first one is an Self Attention Layer and the second one is feed-forward neural network. For each of the sub-layer, it further applies a residual connection and a layer normalization. Mathematically, it could be expressed as follows:

x = layerNorm(x + SelfAttention(x))
x = layerNorm(x + FeedForward(x))

Self Attention Layer

I understand what attention layer tries to do by reading from “Neural Machine Translation by Jointly Learning to Align and Translate”. For a given sequence [x1, ... xn], self-attention mechanism is trying to figure out how much weight each token x_i should contribute to the output and do a weight sum of tokens [x1, ... xn]. To implement this, self attention layer has three basic elements which are Q, K, V where Q stands for queries, K stands for keys and V stands for values. So, Q and K will be used to compute the weight matrix and do a weighted sum of V. Mathematically, it could be expressed as

softmax(QK^T)V

In practice, to avoid generating too big numbers when Q and K are multiplied together, it is recommended to do a scaled self-attention which is

softmax(QK^T / sqrt(d_k))V, where d_k is the dimension of values.

Multi-head Attention Layer

Instead of just using one set of Q, K, V matrix, the attention layer splits the Q, K and V matrixs into h smaller matrixs Qi, Ki and Vi where i is from 1 to h. Each set of Qi, Ki, and Vi is called as one head of the attention layer and the final result will be concatanating the results from these h heads. So, although the mathematical computations remain the same, these h heads are expected to capture different features from the input. A graph representation is as follows:

Feed-forward Layer

This is just two layers of Perceptron where matematically, it could be described as follows:

y = max(0, x * W1 +b1) * W2 + b2

Position Encoding

To help the model understand the sequential property of the input, the embedding of each token adds up a position encoding information which is expressed as follows:

PE(pos,2i) = sin(pos/10000^(2i/dmodel))
PE(pos,2i+1) = cos(pos/10000^(2i/dmodel))

More information around cos and sin of position encoding could be found from paper.